目次
前回の記事では、「非言語検査」の推論・表の読み取りについての勉強方法をご紹介しました。
今回は集合・場合の数についての勉強方法をご紹介していきます!

非言語検査
(前回のおさらい)
「非言語検査」においては、推論・表の読み取り・集合・場合の数・確率・金額計算・分担計算・速度算・割合が、主な出題単元です。「非言語検査」は数的処理能力や論理的思考力を見られるため、数式の復習と苦手単元の重点的な対策が必要です。
集合
与えられた複数の集合に関する情報をもとに答えを導き出す問題です。数字を視覚的に分かりやすく整理する能力が必要になります。
【例題】
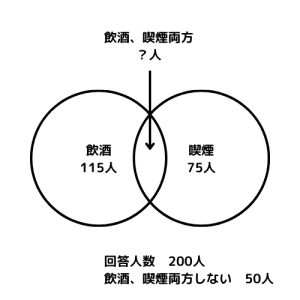
社会人200人を対象に飲酒と喫煙に関するアンケートを行いました。 その結果、飲酒すると答えた人は115人、喫煙すると答えた人は75人でした。 また、飲酒も喫煙も両方しないと答えた人は50人でした。 このとき、飲酒も喫煙も両方すると答えた人は何人でしょうか。
1.10人
2.15人
3.20人
4.25人
5.30人
6.35人
7.40人
8.45人
正解は、7(40人)
【解説】
飲酒も喫煙も両方すると答えた人をXとおき、計算する
115 + 75 – X = 200 – 50
X = 40(人)
《勉強方法》
ベン図を活用すると、簡単に問題を解けるようになります。まずは使い方を覚えましょう。
ベン図
円を使って複数の数字を視覚的に整理します。例題を使うと、このような図になります。問題が変わっても図は変わりません。?の部分が変わるだけです。どこの数字を聞かれても答えられるように、ベン図を理解しておきましょう。視覚的に整理するための方法なので、見やすいように丁寧に書くこともポイントです。
場合の数
「~する場合どうなるか?」というあらゆる選択肢の中から指定された状況における答えを導き出す問題です。
【例題】
1桁の数字が書かれたA、B、C、Dの4枚のカードがあります。この4枚から3枚を並べて3桁の整数を作るとき、何通りの作り方がありますか。
1.3通り
2.6通り
3.9通り
4.12通り
5.24通り
6.36通り
7.48通り
8.52通り
正解は、5(24通り)
【解説】
1枚目の選択肢は4通り、2枚目の選択肢は3通り(1枚目で使ったカード以外)、3枚目の選択肢は2通り(1,2枚目で使ったカード以外)、4枚目の選択肢は1通り。
4 × 3 × 2 × 1 = 24(通り)
順列の公式に当てはめると、
4P3 = 4 × 3 × 2 × 1 = 24(通り)
《勉強方法》
ほとんどの問題は順列と組合せの公式によって、答えを導き出すことができます。高校数学で習う単元ですが、忘れている場合はまず公式の使い方を思い出しましょう。次に、10問ほどを繰り返し解くことで、公式の使い方や考え方に慣れていきましょう。
順列
異なるn個のものからr個選び並べる場合の総数は、
![]()
組合せ
異なるn個のものからr個選ぶ場合の総数は、
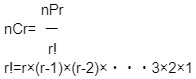
>>SPIの勉強方法(確率・金額計算)
次回移行、数学の問題が出題される「非言語検査」の勉強方法の続き(確率・金額計算・分担計算・速度算・割合)をご紹介します!
(本記事の参考サイト)
・SPI対策問題集 produced by CareerMine
https://spi.careermine.jp/
・SPI無料学習サイト produced by StudyPro
https://saisokuspi.com/







